Draw a line parallel to the hypotenuse $BC$ from the vertex $A$ of the right isosceles triangle $ABC$, and place a point $D$ on it so that $BD=BC$.

Let $E$ be the intersection point of $BD$ and $AC$. Then,
$$CD=CE.$$

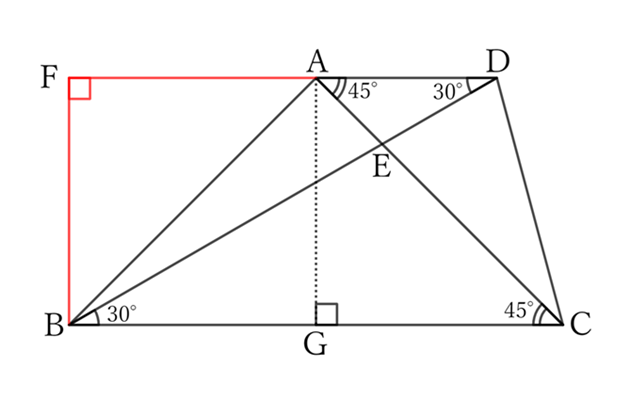
If the intersection point of the extension of $DA$ and the line that passes through $B$ and is perpendicular to $BC$ is $F$, then
$$∠DFB=∠R.$$

Since $BF=AG$,
$$BF=\frac{1}{2} BC,$$
$$∴ \ BF=\frac{1}{2} BD.$$

Therefore, $△BDF$ is a right triangle of $30°-60°-90°$ type,
$$∠BDF=30°.$$

Since $BC∥AD$,
$$∠DBC=30°.$$

Since $△BCD$ is an isosceles triangle with $B$ as a vertex,
$$∠BDC=\frac{1}{2} (180°-30°)=75°,$$
$$∴ \ ∠CDE=75°. \qquad [1]$$

Since $BC∥AD$,
$$∠ACB=∠CAD,$$
$$∴ \ ∠CAD=45°,$$
$$∴ \ ∠EAD=45°.$$

Then, since $∠CED$ is an exterior angle of $△EAD$,
$$∠CED=45°+30°=75°. \qquad [2]$$
From $[1]$ and $[2]$, $△CDE$ is an isosceles triangle with $C$ as the vertex. Thus,
$$CD=CE.$$

$ $