In a rectangular triangle $ABC$ with $∠A$ as a right angle, if $D$ and $E$ are placed on the hypotenuse $BC$ such that $BD=AB$ and $CE=AC$, then $∠CAD$ and $∠BAE$ are equal to half of $∠B$ and $∠C$ respectively.
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$Solution
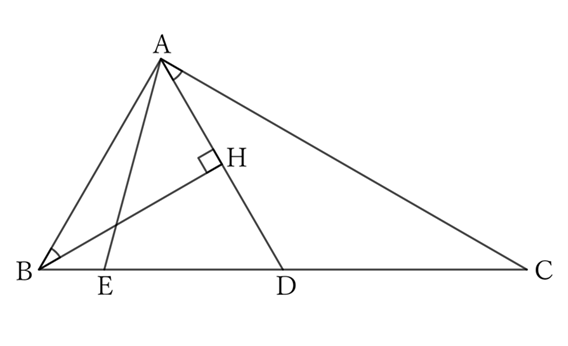
Let $H$ be the foot of the perpendicular line from $B$ to $AD$.
First,
$$∠CAD+∠DAB \ (=∠A) \ =∠R.$$
However, for $△ABH$,
$$∠ABH+∠HAB=∠R,$$
$$∠DAB=∠HAB,$$
$$∴ \ ∠ABH+∠DAB=∠R,$$
$$∴ \ ∠CAD=∠ABH.$$
Then, since $BD=AB$, $△BAD$ is an isosceles triangle with $B$ as its vertex.
Thus, $BH$ is the bisector of $∠B$.
$$∴ \ ∠ABH=\frac{1}{2}∠B,$$
$$∴ \ ∠CAD=\frac{1}{2}∠B.$$
Next, since $CE=AC$, $△CAE$ is C is an isosceles triangle with $C$ as its vertex. Therefore,
$$∠CAE=∠CEA=∠R-\frac{1}{2}∠C.$$
Then,
$$∠A=∠BAE+∠CAE=∠R,$$
$$∴ \ ∠BAE+∠R-\frac{1}{2}∠C=∠R,$$
$$∴ \ ∠BAE=\frac{1}{2}∠C.$$
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.31.