In a rectangular triangle $ABC$, let $F$ be the intersection point of the perpendicular line $BE$ drawn from the right-angled vertex $B$ to $AC$ and the bisector $AD$ of $∠A$, and let $G$ be the intersection point of $BC$ with a line passing through $F$ and parallel to $AC$. Then,
$$BF=BD=GC.$$

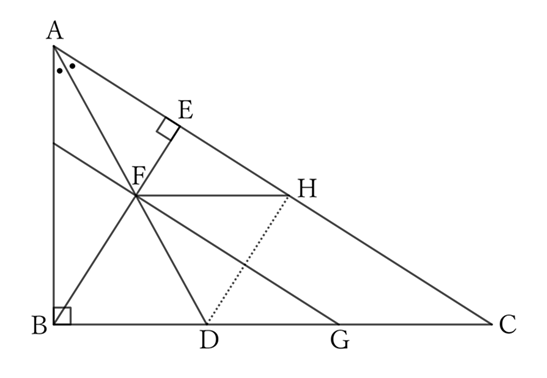
First,
$$∠EAF=∠BAD \qquad and \qquad ∠AEF=∠ABD \ (=∠R),$$
$$∴ \ △AEF \sim △ABD,$$
$$∴ \ ∠AFE=∠ADB \ (=∠FDB).$$
However, $∠AFE$ and $∠DFB$ are opposite angles,
$$∠AFE=∠DFB,$$
$$∴ \ ∠FDB=∠DFB.$$
Therefore, $△BDF$ is an isosceles triangle with $B$ as its vertex,
$$BF=BD. \qquad [1]$$
If $H$ is the intersection point of $AC$ with a line that passes through $F$ and is parallel to $BC$,
$$∠HFD=∠FDB=∠DFB,$$
$$∴ \ ∠BFA=∠HFA.$$
Then, since $△ABF$ and $△AHF$ have the side $AF$ and the angles at both ends are equal,
$$△ABF≡△AHF,$$
$$∴ \ BF=HF.$$
Since $GC∥HF$ and $CH∥FG$, the quadrilateral $GCHF$ is a parallelogram. Thus,
$$GC=HF,$$
$$∴ \ BF=GC. \qquad [2]$$
By $[1]$ and $[2]$,
$$BF=BD=GC.$$

$ $