Problem
Construct squares $ABDE$ and $ACFG$ with the sides $AB$ and $AC$ of a right triangle $ABC$ with $∠B=∠R$, and let $H$ be the intersection point between the extension of $BA$ and $EG$. Then,
$$BC=2AH.$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
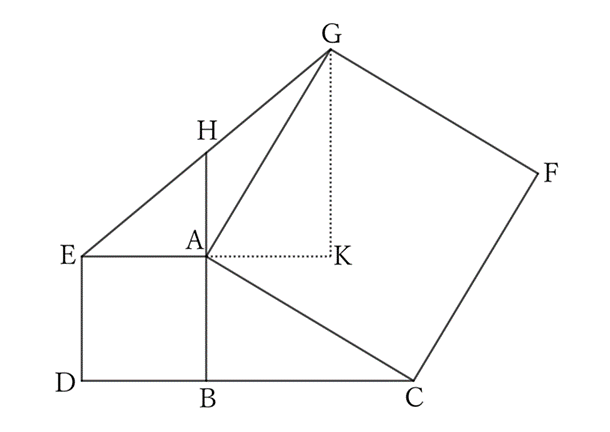
Extend $EA$ and take a point $K$ such that $AB=AK$. Then,
$$AC=AG \qquad and \qquad ∠CAB=∠GAK,$$
$$∴ \ △ABC≡△AKG,$$
$$∴ \ ∠AKG=∠ABC=∠R.$$
For $△GEK$, $A$ is the midpoint of $EK$, and since $AH∥KG$,
$$KG=2AH.$$
Moreover, since $△ABC≡△AKG$,
$$KG=BC,$$
$$∴ \ BC=2AH.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.31.