In a right isosceles triangle $ABC$ with $∠B=∠R$, let $D$ and $E$ be the feet of the perpendicular lines drawn from a point $P$ on hypotenuse $AC$ to $AB$ and $AC$, respectively, and $F$ be the foot of the perpendicular line drawn from $P$ to $DE$.

Then, the line $PF$ always passes through a fixed point.

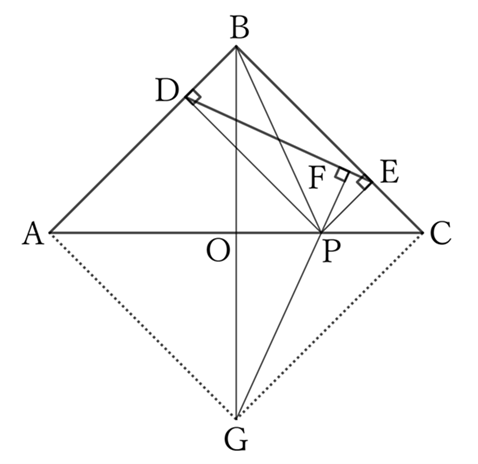
Let $O$ be the midpoint of the side $AC$, and $G$ be the intersection of the two lines $BO$ and $FP$.

Since the quadrilateral $BEPD$ is a rectangle and $△DEP \sim △PEF$,

$$∠PDE=∠FPE,$$

$$∴ \ ∠DPB=∠FPE.$$

Since $△DAP \sim △EPC$ and $∠DPA=∠EPC \ (=45°)$,

$$(∠DPB+∠DPA=) \ ∠APB=∠CPF \ (=∠FPE+∠EPC),$$

$$∴ \ ∠APB=∠APG, \qquad (∵ ∠CPF=∠APG)$$

$$∴ \ △APB≡△APG,$$

$$∴ \ AB=AG.$$

Therefore, the quadrilateral $ABCG$ is a square, and the line $PF$ always passes through the fixed point $G.$

$ $