If we draw squares $BCDE$ and $ACFG$ with the sides $BC$ and $AC$ of a right-angled triangle $ABC$ with $∠B=∠R$ outside the triangle, and the intersection point of the lines $DF$ and $BC$ is $H$, then
$$AB=2CH.$$

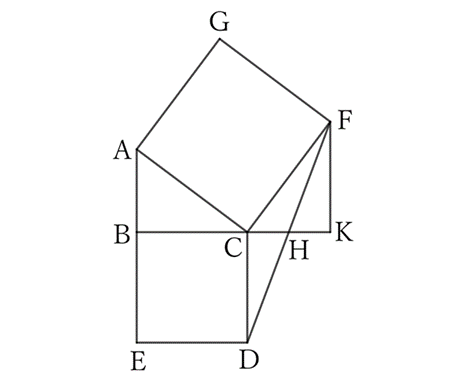
If the foot of the perpendicular line from $F$ to the line $BC$ is $K$, then

$$AC=CF, \qquad ∠ACB=∠CFK \qquad and \qquad ∠ABC=∠CKF \ (=∠R),$$
$$∴ \ ⊿ABC≡⊿CKF,$$
$$∴ \ AB=CK. \qquad \qquad [1]$$

Besides,

$$CD∥KF,$$
$$∴ \ ∠CDH=∠KFH.$$
Furthermore,
$$CD=KF \qquad and \qquad ∠DCH=∠FKH \ (=∠R),$$
$$∴ \ ⊿DCH≡⊿FKH,$$
$$∴ \ CH=KH,$$
$$∴ \ CK=2CH. \qquad [2]$$
From $[1]$ and $[2]$,
$$AB=2CH.$$

$ $