Problem
The medians drawn from both ends of the base of an isosceles triangle to the opposite sides are equal.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
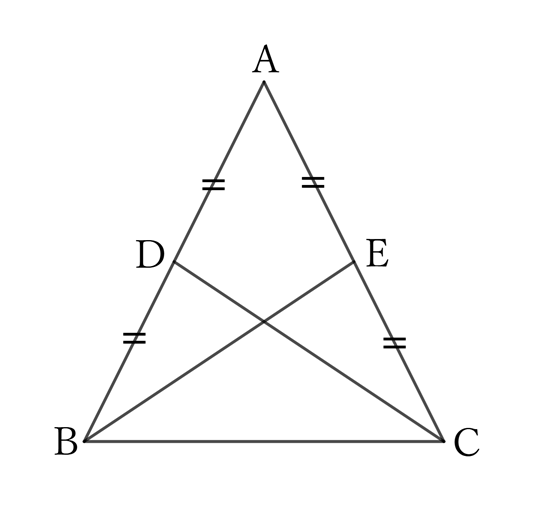
$△DBC$ and $△ECB$ share the side $BC \ (=CB)$,
$$DB=EC \qquad (∵ \ AB=AC, \quad DB=\frac{1}{2} AB \quad and \quad EC=\frac{1}{2} AC)$$
$$and \qquad ∠DBC=∠ECB \qquad (∵ \ ∠B=∠C),$$
$$∴ \ △DBC≡△ECB,$$
$$∴ \ CD=BE.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.32.