Problem
If the bisectors of $∠B$ and $∠C$ of a triangle $ABC$ are equal, then the triangle is isosceles.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
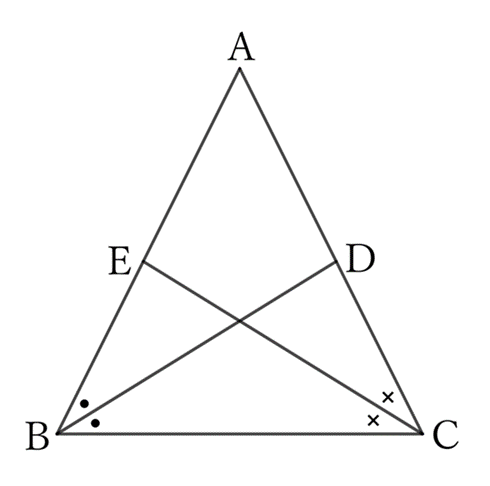
If we assume that $∠B>∠C$, then from the problem $0080$,
$$BD<CE.$$
Similarly, if we assume that $∠B<∠C$,
$BD>CE$.
Therefore, if $BD=CE$,
$$∠B=∠C.$$
$$BD<CE.$$
Similarly, if we assume that $∠B<∠C$,
$BD>CE$.
Therefore, if $BD=CE$,
$$∠B=∠C.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.32.