Problem
Let the vertex angle $A$ of an isosceles triangle $ABC$ be $120°$.
Let $D$ be the foot of the perpendicular line drawn from the vertex angle $A$ to $BC$, and take any point $P$ on $AD$ and connect it to $B$ and $C$.
The following inequality holds:
$$AP+BP+CP>AB+AC.$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
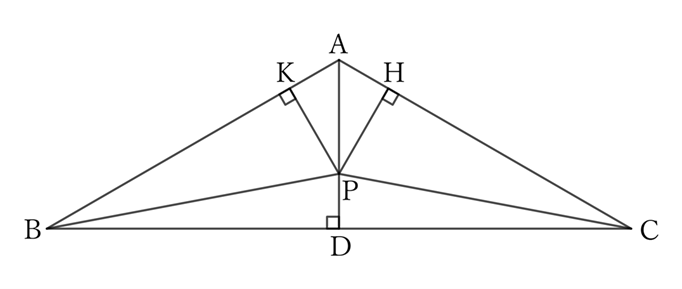
Let $K$ and $H$ be the feet of the perpendicular lines drawn from $P$ to $AB$ and $AC$, respectively.
$△AKP$ and $△AHP$ share the side $AP$,
$$∠AKP=∠AHP=90°, \qquad ∠PAK=∠PAH=60°$$
$△AKP$ and $△AHP$ share the side $AP$,
$$∠AKP=∠AHP=90°, \qquad ∠PAK=∠PAH=60°$$
$$and \qquad ∠KPA=∠HPA=30°,$$
$$∴ \ △AKP≡△AHP,$$
$$∴ \ AK=AH=\frac{1}{2} AP,$$
$$∴ \ AP=AK+AH. \qquad [1]$$
For $△PKB$ and $△PHC$,
$$∠PKB=∠PHC=∠R,$$
$$∴ \ BP>KB \qquad and \qquad CP>HC. \qquad [2]$$
From $[1]$ and $[2]$,
$$AP+BP+CP>AK+AH+KB+HC,$$
$$∴ \ AP+BP+CP>(AK+KB)+(AH+HC),$$
$$∴ \ AP+BP+CP>AB+AC.$$
$$∴ \ △AKP≡△AHP,$$
$$∴ \ AK=AH=\frac{1}{2} AP,$$
$$∴ \ AP=AK+AH. \qquad [1]$$
For $△PKB$ and $△PHC$,
$$∠PKB=∠PHC=∠R,$$
$$∴ \ BP>KB \qquad and \qquad CP>HC. \qquad [2]$$
From $[1]$ and $[2]$,
$$AP+BP+CP>AK+AH+KB+HC,$$
$$∴ \ AP+BP+CP>(AK+KB)+(AH+HC),$$
$$∴ \ AP+BP+CP>AB+AC.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.33.