Let $Q$ and $R$ be the points where the perpendicular line passing through any point $P$ on the base $BC$ of an isosceles triangle $ABC$ with vertex $A$ intersects with the sides $AB$ and $AC$ (or their extensions), respectively.

Then, if $PQ+PR$ is always equal to the side $BC$,

$$∠A=∠R.$$

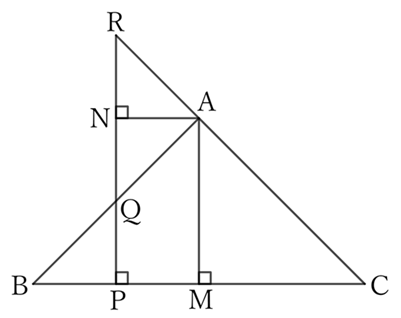
If perpendicular lines $AM$ and $AN$ are drawn from $A$ to $BC$ and $QR$ respectively, $AMPN$ is a rectangle. Thus,

$$PN=AM. \qquad [1]$$

Since $△BPQ$ and $△CPR$ are right-angled triangles and $∠B=∠C$,

$$∴ \ ∠BQP=∠CRP,$$

$$∴ ∠AQR=∠ARQ.$$

And since $AN⊥QR$,

$$NQ=NR. \qquad [2]$$

From $[1]$ and $[2]$,
$$PQ+PR=(AM-NR)+(AM+NR)=2AM.$$

However, from the problem statement,
$$PQ+PR=BC,$$
$$∴ \ 2AM=BC,$$
$$∴ \ BM=AM=CM.$$

Therefore, since $A$ is on the circumference of a circle in which centre is $M$ and diameter is $BC$,

$$∠A=∠R.$$

$ $