If perpendicular lines $PD$ and $PE$ are dropped from any point $P$ on the base $BC$ of an isosceles triangle $ABC$ with $A$ as its vertex to the sides $AB$ and $AC$, then $AD+AE$ is constant.

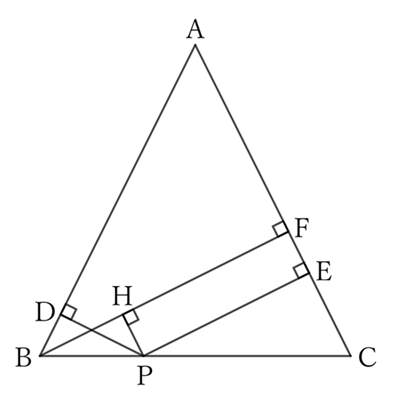
If we draw a perpendicular line $BF$ from $B$ to $AC$ and a perpendicular line $PH$ from $P$ to $BF$, then $PHFE$ is a rectangle. Thus,
$$HP=EF.$$
$△DBP$ and $△HPB$ share the side $BP \ (=PB)$.
$$∠DBP (=∠B)=∠C \qquad and \qquad HP∥AC,$$

$$∴ \ ∠DBP=∠HPB.$$

Furthermore,

$$∠BDP=∠PHB \ (=∠R),$$
$$∴ \ △DBP≡△HPB,$$
$$∴ \ DB=HP,$$
$$∴ \ DB=EF,$$
$$∴ \ AD+AE=AB+AF.$$
Therefore, wherever $P$ is placed on $BC$, $AD+AE$ is equal to the constant $AB+AF$.

$ $