Let $E$ and $F$ be the points where the line that passes through a point $D$ on the base $BC$ of an isosceles triangle $ABC$ and is perpendicular to $BC$ intersects with $AB$ and $AC$ (or their extensions).

Construct rectangles $EDBG$ and $FDCH$, and let $S$ and $T$ be the midpoints of $DG$ and $DH$ respectively.

Then, the intersection $O$ of $GT$ and $HS$ is on the line connecting $A$ and $D$.

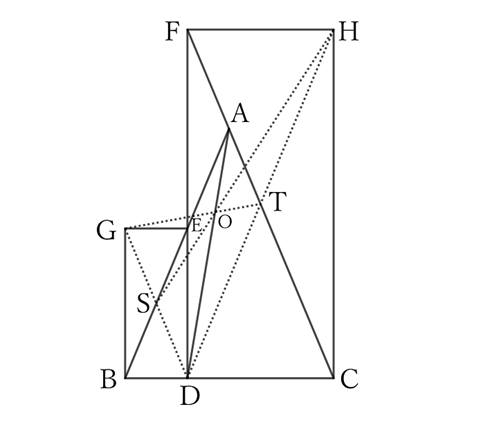
From the diagram,

$$GD∥AC \qquad and \qquad DH∥AB,$$

$$∴ \ AT∥DS \qquad and \qquad AT=DS,$$

However,

$$AT∶DG=1∶2 \qquad and \qquad △ATO∼△DGO,$$

$$∴ \ AO∶DO=1∶2.$$

Therefore, $GT$ passes through the point $O$ which divides $AD$ into $1∶2$.

Similarly,

$$AS=TD, \qquad AS∶HD=1∶2, \qquad and \qquad △AOS∼△DOH,$$

$$∴ \ AO∶DO=1∶2.$$

Therefore, $HS$ passes through the point $O$ which divides $AD$ into $1∶2$.

In other words, the intersection $O$ of $GT$ and $HS$ is on $AD$.

$ $