Problem
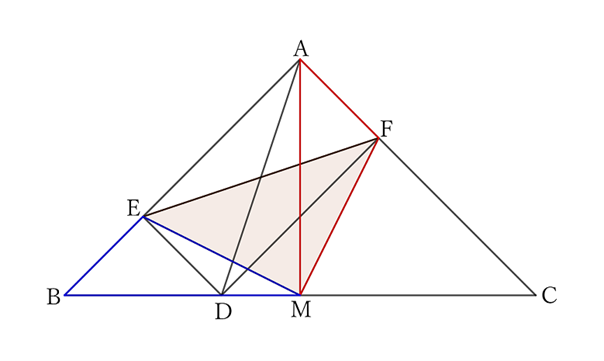
Let $DE$ and $DF$ be the perpendicular lines drawn from any point $D$ on the hypotenuse $BC$ of a right isosceles triangle $ABC$ to the sides $AB$ and $AC$, respectively, and let $M$ be the midpoint of BC.
Then $△EMF$ is also an isosceles right triangle.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
$$AF=ED \qquad and \qquad ED=BE,$$
$$∴ AF=BE. \qquad [1]$$
Furthermore,
$$AM=BM \qquad and \qquad ∠FAM=∠EBM \ (=45°). \qquad [2]$$
From $[1]$ and $[2]$,
$$∴ \ △AFM≡△BEM. \qquad [3]$$
From $[3]$,
$$∠FMA=∠EMB,$$
$$∴ \ ∠EMF=∠AMB-∠EMB+∠FMA=90°. \qquad [4]$$
From $[3]$,
$$MF=ME. \qquad [5]$$
From $[4]$ and $[5]$, $△EMF$ is a right-angled isosceles triangle.
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.35.