Problem
$O$ is a point in an equilateral triangle $ABC$.
If $∠BAO>∠CAO$, then
$$∠BCO>∠CBO.$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
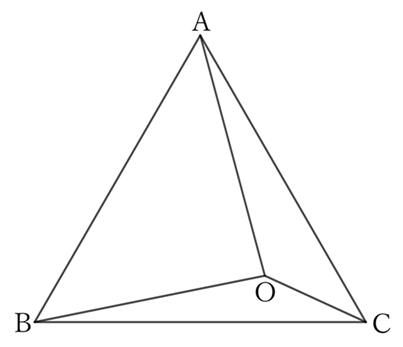
$△ABO$ and $△ACO$ share the side $AO$,
$$AB=AC \qquad and \qquad ∠BAO>∠CAO,$$
$$∴ \ BO>CO,$$
$$∴ \ ∠BCO>∠CBO.$$
$$AB=AC \qquad and \qquad ∠BAO>∠CAO,$$
$$∴ \ BO>CO,$$
$$∴ \ ∠BCO>∠CBO.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.36.