Problem
Divide the line segment $AB$ at $C$ and construct equilateral triangles $ACP$ and $BCQ$ on $AC$ and $BC$.
Then, the sum of the heights of the two triangles is constant.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
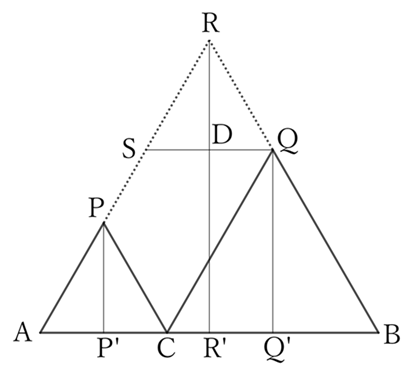
Let $R$ be the intersection point of the extensions of $AP$ and $BQ$, and place $S$ on $AR$ so that $AB∥QS$.
Since $PCQR$ is a parallelogram,
$$PC=RQ.$$
Similarly, since $ACQS$ is also a parallelogram,
$$AC=SQ.$$
Since $AC∥SQ$ and $PC∥RQ$,
$$∠PCA=∠RQS,$$
$$∴ \ △PAC≡△RSQ,$$
$$∴ \ PP’=RD. \qquad [1]$$
Since $AB∥QS$,
$$QQ’=DR’. \qquad [2]$$
From $[1]$ and $[2]$,
$$PP’+QQ’=RD+DR’=RR’.$$
Therefore, no matter where $C$ is placed on $AB$, the sum of the heights of $△ACP$ and $△BCQ$ is constant.
$$PC=RQ.$$
Similarly, since $ACQS$ is also a parallelogram,
$$AC=SQ.$$
Since $AC∥SQ$ and $PC∥RQ$,
$$∠PCA=∠RQS,$$
$$∴ \ △PAC≡△RSQ,$$
$$∴ \ PP’=RD. \qquad [1]$$
Since $AB∥QS$,
$$QQ’=DR’. \qquad [2]$$
From $[1]$ and $[2]$,
$$PP’+QQ’=RD+DR’=RR’.$$
Therefore, no matter where $C$ is placed on $AB$, the sum of the heights of $△ACP$ and $△BCQ$ is constant.
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.36.