Problem
If equilateral triangles $BCX$ and $CDY$, with the bases $BC$ and $CD$ of a parallelogram $ABCD$, are drawn outside the quadrilateral, then $△AXY$ becomes an equilateral triangle.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
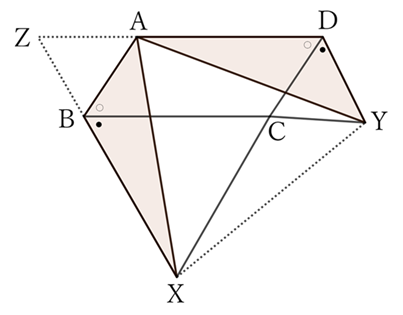
For $△ABX$ and $△YDA$,
$$AB=YD, \qquad BX=DA \qquad and \qquad ∠ABX=∠YDA,$$
$$∴ \ △ABX≡△YDA,$$
$$∴ \ XA=AY. \qquad [1]$$
However, since $ZD∥BC$ and $∠CBX$ and $∠Z$ are corresponding angles, for $△ABX$ and $△YDA$, the angle between corresponding sides $BX$ and $DA$ is
$$∠Z=60°.$$
Therefore, the angle between corresponding sides $AX$ and $YA$ is also
$$∠XAY=60°. \qquad [2]$$
From $[1]$ and $[2]$, $△AXY$ is an equilateral triangle.
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, pp.36-37.