Problem
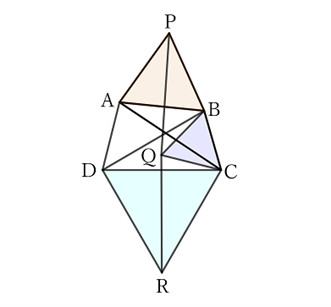
Draw equilateral triangles $ABP$ and $CDR$ with opposite sides $AB$ and $CD$ on the outside of the quadrilateral $ABCD$.
When drawing an equilateral triangle with side $BC$ as the base inside the quadrilateral,
$$PQ=AC \qquad and \qquad QR=BD.$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
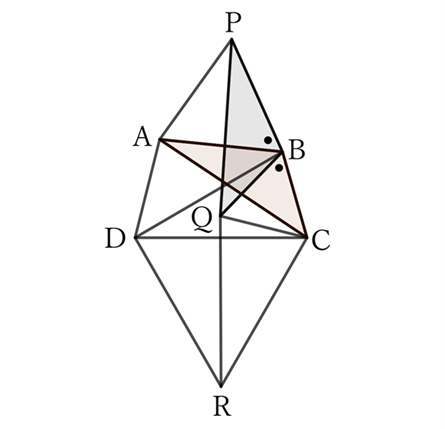
For $△ABC$ and $△PBQ$,
$$AB=PB, \qquad BC=BQ \qquad and \qquad ∠ABC=∠ABQ+60°=∠PBQ,$$
$$∴ \ △ABC≡△PBQ,$$
$$∴ \ AC=PQ.$$
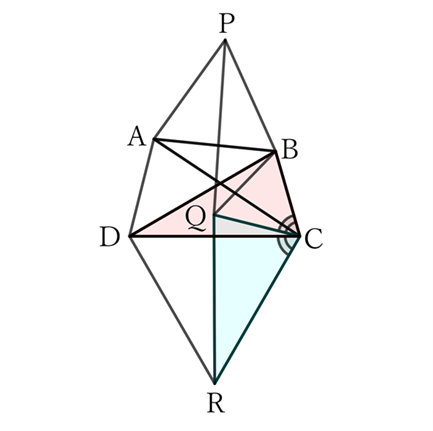
For $△BCD$ and $△QCR$,
$$BC=QC, \qquad CD=CR \qquad and \qquad ∠BCD=∠QCD+60°=∠QCR,$$
$$∴ \ △BCD≡△QCR,$$
$$∴ \ BD=QR.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.37.