The sum of the lengths of the perpendiculars $PE, \ PF$ and $PG$ from any point $P$ in an equilateral triangle $ABC$ to sides $BC, \ CA$ and $AB$ is constant.
Moreover, what if $P$ is outside the equilateral triangle $ABC$?
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$Solution
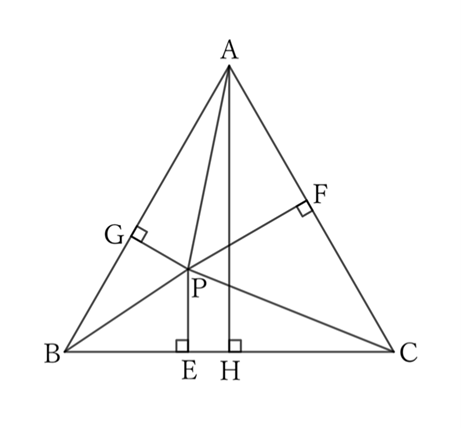
The area of the triangle $ABC$ is the sum of the areas of the triangles $BCP, \ CAP$ and $ABP$.
Thus,
$$\frac{1}{2}×BC×PE+\frac{1}{2}× CA×PF+\frac{1}{2}×AB×PG=\frac{1}{2}×BC×AH,$$
$$∴ \ BC×PE+CA×PF+AB×PG=BC×AH.$$
However, since $BC=CA=AB$,
$$BC×(PE+PF+PG)=BC×AH,$$
$$∴ \ PE+PF+PG=AH.$$
In other words, as long as $P$ is within the equilateral triangle $ABC$, $PE+PF+PG$ is constant regardless of its position.
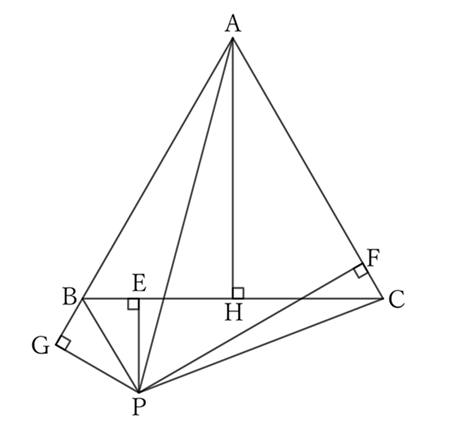
If $P$ is below $BC$, the area of the triangle $ABC$ is the sum of the areas of the triangles $ACP$ and $ABP$ minus the area of the triangle $PCB$.
Therefore,
$$\frac{1}{2}×CA×PF+\frac{1}{2}×AB×PG-\frac{1}{2}×BC×PE=\frac{1}{2}×BC×AH,$$
$$∴ \ CA×PF+AB×PG-BC×PE=BC×AH.$$
However, since $BC=CA=AB$,
$$BC×(PF+PG-PE)=BC×AH,$$
$$∴ \ PF+PG-PE=AH.$$
Similarly, if $P$ is to the right of $CA$,
$$PE+PG-PF=AH.$$
If $P$ is to the left of $AB$,
$$PE+PF-PG=AH.$$
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.37.