Problem
If $D$ and $E$ are the points that trisect the side $BC$ of triangle $ABC$, then
$$AB+AC>AD+AE.$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
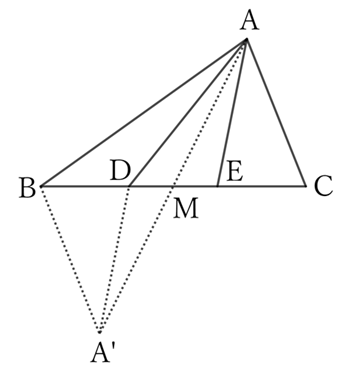
If the midpoint of $BC$ is $M$, and $AM$ is extended to the point $A’$ such that $AM=MA’$, then
$$AC=BA’ \qquad and \qquad AE=DA’,$$
$$∴ \ AB+AC=AB+BA’ \qquad and \qquad AD+AE=AD+DA’.$$
However, from the problem $0046$,
$$AB+BA’>AD+DA’,$$
$$∴ \ AB+AC>AD+AE.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.39.