There are two half lines $OX$ and $OY$ starting at $O$.

Let a point $P$ be within $∠XOY$ and the feet of perpendicular lines drawn from it to $OX$ and $OY$ be $Q$ and $S$, respectively.

Then, if the difference between $PS$ and $PQ$ is a constant $m$, then the point $P$ is always on a fixed straight line.

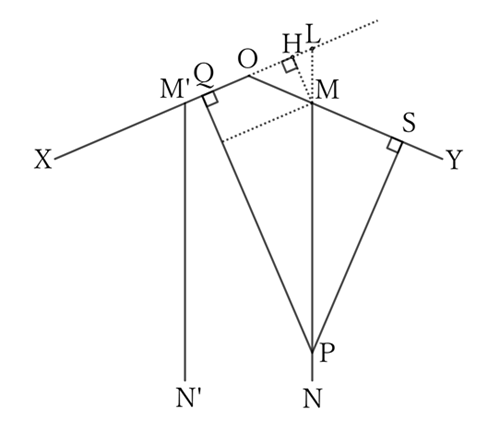
Draw a line through $P$ so that the angles which the line makes with the extension of $XO$ and $YO$ are equal.

Let the points where the line intersects with the extension of $XO$ and $YO$ be $L$ and $M$, respectively.

If a perpendicular line $MH$ is drawn from $M$ to $OL$, then from the problem $0152$,

$$PQ-PS=MH.$$

However, since $PQ-PS=m$ (a constant) by assumption, $MH=m$ is constant.

Therefore, the position of $M$ is determined by drawing a parallel line at a distance of $m$ from $OX$.

Thus, the isosceles triangle $OML$ is a definite triangle, and $P$ is on the half line $MN$, which is an extension of the definite line segment $ML$.

However, note that $P$ may lie on the half line $M’ N’$ that is symmetric with $MN$ with respect to the bisector of $∠XOY$.

$ $