In a triangle $ABC$, suppose $AC>AB$.

Let $D$ be a point on $CA$ such that $CD=AB$, $E$ be the midpoint of $AD$, $F$ be the midpoint of $BC$, and $G$ be the point where the extension of $FE$ intersects with the extension of $BA$, then

$$AE=AG.$$

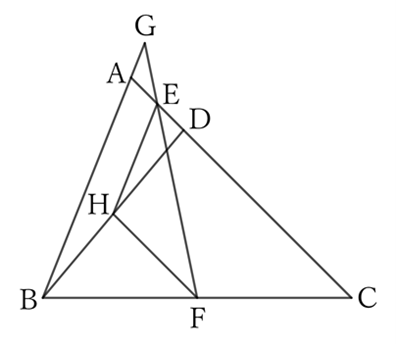
If the midpoint of $BD$ is $H$, then

$$AB∥EH \qquad and \qquad AB:EH=2:1.$$

Furthermore,

$$CD∥FH \qquad and \qquad CD:FH=2:1.$$

Since $CD=AB$,

$$EH=FH.$$

Therefore, since $△HEF$ is an isosceles triangle with $H$ as a vertex,

$$∠HEF=∠HFE.$$

Since $GB∥EH$,

$$∠AGE=∠HEF.$$

Since $AC∥HF$,

$$∠AEG=∠HFE,$$

$$∴ \ ∠AGE=∠AEG. \qquad (∵ \ ∠HEF=∠HFE)$$

Therefore, since $△AGE$ is an isosceles triangle with $A$ as a vertex,

$$AG=AE.$$

$ $