Problem
The perimeter of a quadrilateral is greater than the sum of its diagonals but less than twice the sum.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
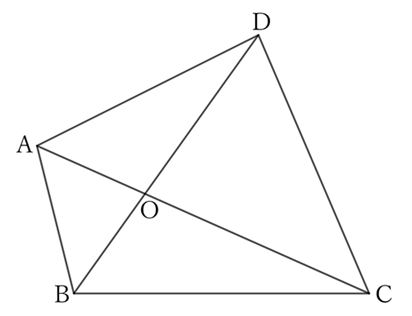
For $△ABC$ and $△ACD$,
$$AC<AB+BC,$$
$$AC<CD+DA,$$
$$BD<BC+CD,$$
$$BD<AB+DA,$$
$$∴ \ 2(AC+BD)<2(AB+BC+CD+DA),$$
$$∴ AC+BD<AB+BC+CD+DA \qquad [1]$$
If the intersection of both diagonals is $O$,
$$AB<AO+BO,$$
$$BC<BO+CO,$$
$$CD<CO+DO,$$
$$DA<DO+AO,$$
$$∴ \ AB+BC+CD+DA<2(AO+BO+CO+DO),$$
$$∴ \ AB+BC+CD+DA<2(AC+BD). \qquad [2]$$
From $[1]$ and $[2]$,
$$AC+BD<AB+BC+CD+DA<2(AC+BD).$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.41.