Problem
If the longest side of a quadrilateral $ABCD$ is $AD$ and the shortest side is $BC$, then $∠BCD$ is greater than $∠BAD$ and $∠ABC$ is greater than $∠ADC$:
$$∠BCD>∠BAD \qquad and \qquad ∠ABC>∠ADC.$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
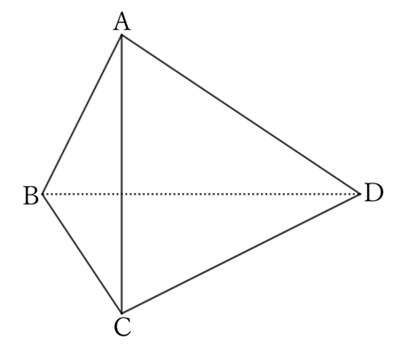
Since $AD$ is the largest side,
$$AD>CD,$$
$$∴ \ ∠DCA>∠DAC. \qquad [1]$$
Since $BC$ is the smallest side,
$$AB>BC,$$
$$∴ \ ∠BCA>∠BAC. \qquad [2]$$
From $[1]$ and $[2]$,
$$∠DCA+∠BCA>∠DAC+∠BAC,$$
$$∴ \ ∠BCD>∠BAD.$$
Similarly,
$$AD>AB,$$
$$∴ \ ∠ABD>∠ADB. \qquad [3]$$
$$CD>BC,$$
$$∴ \ ∠CBD>∠CDB. \qquad [4]$$
From $[3]$ and $[4]$,
$$∠ABD+∠CBD>∠ADB+∠CDB,$$
$$∴ \ ∠ABC>∠ADC.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.42.