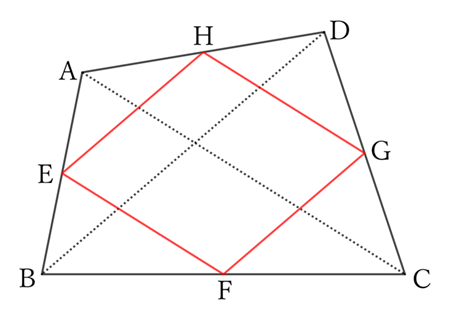
$△ADB$ and $△AHE$ share $∠A$,

$$BA∶EA=AD∶AH=2∶1,$$

$$∴ \ △ADB∼△AHE,$$

$$∴ \ ∠DBA=∠HEA,$$

$$∴ \ DB∥HE, \qquad [1]$$

$$and \qquad DB∶HE=2:1,$$

$$∴ \ HE=\frac{1}{2} DB. \qquad [2]$$

$△BCD$ and $△FCG$ share $∠C$,

$$BC∶FC=CD∶CG=2∶1,$$

$$∴ \ △BCD∼△FCG,$$

$$∴ ∠CDB=∠CGF,$$

$$∴ \ DB∥GF, \qquad [3]$$

$$and \qquad DB∶GF=2∶1,$$

$$∴ \ GF=\frac{1}{2} DB. \qquad [4]$$

From $[1]$ and $[3]$,

$$HE∥GF. \qquad [5]$$

$△ABC$ and $△EBF$ shares $∠B$,

$$AB∶EB=BC∶BF=2∶1,$$

$$∴ \ △ABC∼△EBF,$$

$$∴ \ ∠BCA=∠BFE,$$

$$∴ \ AC∥EF, \qquad [6]$$

$$and \qquad AC:EF=2:1,$$

$$∴ \ EF=\frac{1}{2} AC. \qquad [7]$$

$△ACD$ and $△HGD$ share $∠D$,

$$CD∶GD=DA∶DH=2∶1,$$

$$∴ \ △ACD∼△HGD,$$

$$∴ \ ∠DAC=∠DHG,$$

$$∴ \ AC∥HG, \qquad [8]$$

$$and \qquad AC:HG=2:1,$$

$$∴ \ HG=\frac{1}{2} AC. \qquad [9]$$

From $[6]$ and $[8]$,

$$EF∥HG. \qquad [10]$$

From $[5]$ and $[10]$, the quadrilateral $EFGH$ is a parallelogram.

Also, from $[2], \ [4], \ [7]$ and $[9]$,

$$EF+FG+HG+HE=\frac{1}{2} AC+\frac{1}{2} DB+\frac{1}{2} AC+\frac{1}{2} DB =AC+DB.$$

In other words, the perimeter of the parallelogram is equal to the sum of the two diagonals of the original quadrilateral.