Problem
The line segment joining the midpoints $M$ and $N$ of the two diagonals $BD$ and $AC$ of a quadrilateral $ABCD$ is not less than half the difference between the two opposite sides.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
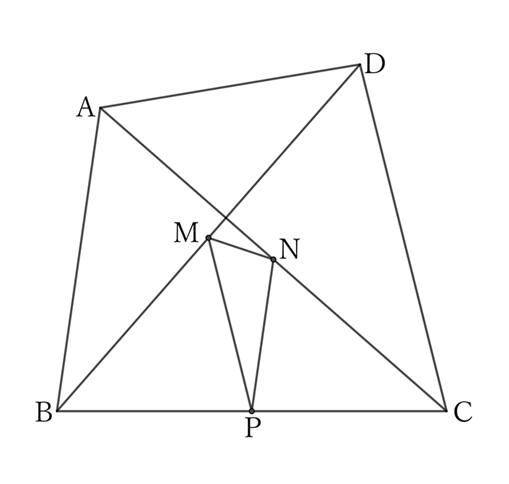
Let $P$ be the midpoint of $BC$.
Then, from the problem $0042$, for $△MPN$,
$$MN>|MP-NP|. \qquad [1]$$
$△BDC$ and $△BMP$ share $∠CBD \ (=∠PBM)$,
$$BD∶BM=BC∶BP=2∶1,$$
$$∴ \ △BDC∼△BMP,$$
$$∴ \ DC∶MP=2∶1,$$
$$∴ \ MP=\frac{1}{2} DC. \qquad [2]$$
$△ACB$ and $△NCP$ share $∠ACB \ (=∠NCP)$,
$$AC∶NC=CB∶CP=2∶1,$$
$$∴ \ △ACB∼△NCP,$$
$$∴ \ AB∶NP=2∶1,$$
$$∴ \ NP=\frac{1}{2} AB. \qquad [3]$$
From $[1], \ [2]$ and $[3]$,
$$MN>\frac{1}{2} |DC-AB|. \qquad [4]$$
Similarly, if the midpoint of $AB$ is $P$,
$$MN>\frac{1}{2} |AD-BC|. \qquad [4]’$$
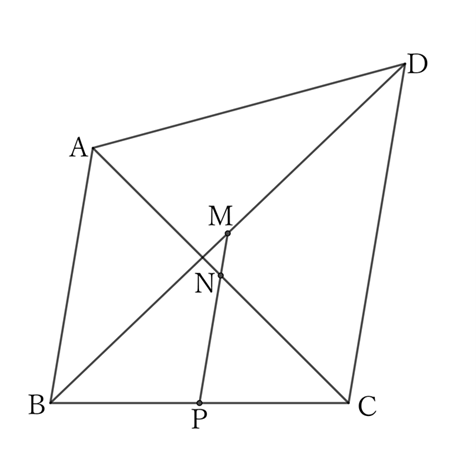
If $AB∥DC$ and the midpoint of $BC$ is $P$, then $M, \ N$ and $P$ are aligned on a straight line. Therefore,
$$MN=|MP-NP|,$$
$$∴ \ MN=\frac{1}{2} |DC-AB|. \qquad [5]$$
Similarly, if $AD∥BC$ and the midpoint of $AB$ is $P$, then $M, \ N$ and $P$ are aligned on a straight line. Thus,
$$MN=\frac{1}{2} |AD-BC|. \qquad [5]’$$
From $[4], \ [4]’, \ [5]$ and $[5]’$,
$$MN≧|DC-AB| \qquad and \qquad MN≧|AD-BC|.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.43.