Problem
The length of the line segment connecting the midpoints $P$ and $Q$ of the opposing sides $AB$ and $CD$ of a quadrilateral $ABCD$ is not greater than half the sum of the lengths of the other two sides $BC$ and $DA$.
If this line segment $PQ$ is equal to the sum of the lengths of $BC$ and $DA$, then the quadrilateral is a trapezoid.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
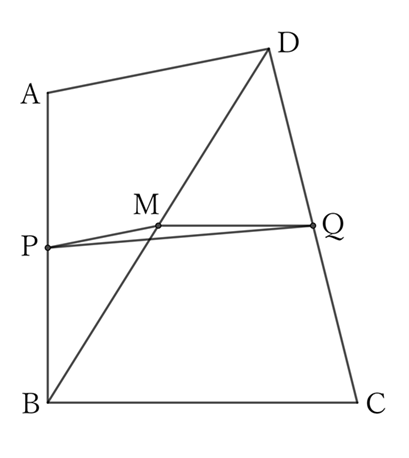
Let $M$ be the midpoint of the diagonal $BD$.
Then, $△CDB$ and $△QDM$ share $∠CDB \ (=∠QDM)$,
$$CD∶QD=DB∶DM=2∶1,$$
$$∴ \ △CDB∼△QDM,$$
$$∴ \ BC∶MQ=2∶1,$$
$$∴ \ MQ=\frac{1}{2} BC. \qquad [1]$$
$△ABD$ and $△PBM$ share $∠ABD \ (=∠PBM)$,
$$AB∶PB=BD∶BM=2∶1,$$
$$∴ \ △ABD∼△PBM,$$
$$∴ \ DA∶MP=2∶1,$$
$$∴ \ MP=\frac{1}{2} DA. \qquad [2]$$
For $△MPQ$,
$$PQ<MP+MQ,$$
$$∴ \ PQ<\frac{1}{2} BC+\frac{1}{2} DA,$$
$$∴ \ PQ<\frac{1}{2} (BC+DA).$$
When $PQ=MP+MQ$,
$P, \ Q$ and $M$ are aligned in a straight line.
Then, since $BC∥AD$, the quadrilateral $ABCD$ is a trapezoid.
Thus,
$$PQ≦\frac{1}{2} (BC+DA).$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.43.