Problem
In a quadrilateral $ABCD$ such that $AB=CD$, if the midpoints of $DA$ and $BC$ are $P$ and $Q$ respectively, and the midpoints of the diagonals $AC$ and $BD$ are $M$ and $N$ respectively, then $PQ$ and $MN$ are perpendicular to each other.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
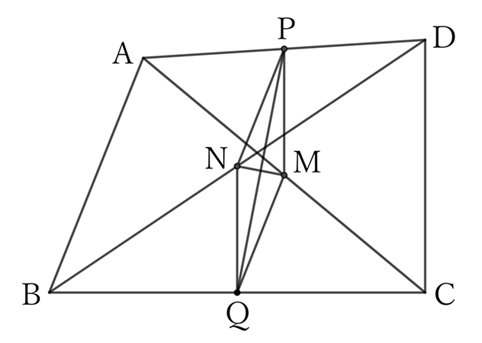
$△ABC$ and $△MQC$ share $∠BCA \ (=QCM)$,
$$BC∶QC=CA∶CM=2∶1,$$
$$∴ \ △ABC∼△MQC,$$
$$∴ \ AB∶MQ=2∶1,$$
$$∴ \ MQ=\frac{1}{2} AB. \qquad [1]$$
Similarly,
$$NP=\frac{1}{2} AB. \qquad [2]$$
$$QN=\frac{1}{2} CD. \qquad [3]$$
$$PM=\frac{1}{2} CD. \qquad [4]$$
Since $AB=CD$,
$$MQ=NP=QN=PM.$$
Therefore, the quadrilateral $MQNP$ is a rhombus and its diagonals are orthogonal.
In other words,
$$PQ⊥MN.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, pp.43-44.