The opposite angles of the quadrilateral formed by the four straight lines that bisect the exterior angles of a quadrilateral are supplementary to each other.

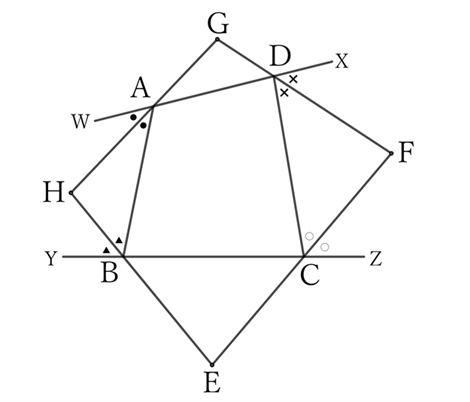
Let $E, \ F, \ G$, and $H$ be the intersection points of the four lines that bisect each of the exterior angles of the quadrilateral $ABCD$.
From the diagram, for the opposite angles $∠F$ and $∠H$ of the quadrilateral $EFGH$,
$$∠F=2∠R-\frac{1}{2} (∠ZCD+∠XDC) \qquad and \qquad ∠H=2∠R-\frac{1}{2} (∠WAB+∠YBA),$$
$$∴ \ ∠F+∠H=4∠R-\frac{1}{2} (∠WAB+∠YBA+∠ZCD+∠XDC).$$
However, since the sum of the four exterior angles of a quadrilateral is four right angles, 
$$∠WAB+∠YBA+∠ZCD+∠XDC=4∠R,$$
$$∴ \ ∠F+∠H=4∠R-2∠R=2∠R,$$
$$∴ \ ∠F=2∠R-∠H \qquad and \qquad ∠H=2∠R-∠F.$$

Therefore, since $∠E+∠G=2∠R$, 

$$∠E=2∠R-∠G \qquad and \qquad ∠G=2∠R-∠E.$$