In a parallelogram,
$(1)$ opposite angles are equal to each other;
$(2)$ opposite sides are equal in length.

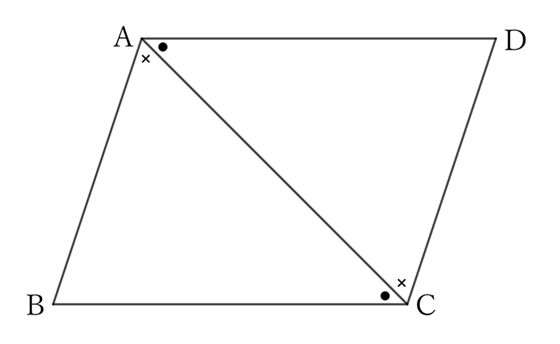
$(1)$

If we draw the diagonal $AC$ on the parallelogram $ABCD$, since $AB∥DC$,
$$∠CAB=∠ACD \qquad and \qquad ∠CAD=∠ACB.$$
However,
$$∠A=∠CAB+∠CAD \qquad and \qquad ∠C=∠ACD+∠ACB,$$
$$∴ \ ∠A=∠C.$$
Similarly, if we draw the diagonal $BD$, we can say:
$$∠B=∠D.$$
Therefore, in a parallelogram, opposite angles are equal to each other.

$(2)$

$△ABC$ and $△CDA$ share the side $CA \ (=AC)$,
$$∠CAB=∠ACD \qquad and \qquad ∠BCA=∠DAC,$$
$$∴ \ △ABC≡△CDA,$$
$$∴ \ AB=CD.$$
Similarly,
$$BC=DA.$$
Therefore, the lengths of the opposite sides of a parallelogram are equal to each other.