If each vertex of a parallelogram $PQRS$ is on each side of another parallelogram $ABCD$, then the diagonals of the two parallelograms pass through the same points.

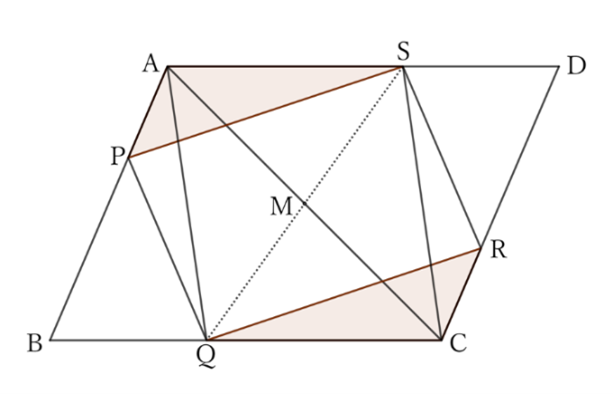
For $△APS$ and $△CRQ$,

$$PS=RQ, \qquad ∠ASP=∠CQR \qquad and \qquad ∠APS=∠CRQ,$$

$$∴ \quad △APS≡△CRQ,$$

$$∴ \quad AS=CQ \qquad and \qquad AS∥CQ.$$

In other words, the quadrilateral $AQCS$ is a parallelogram.

Hence, the diagonal $QS$ passes through the midpoint $M$ of $AC$.

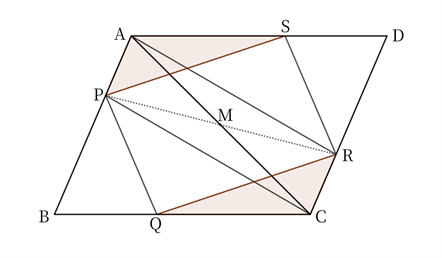
Similarly, since $△APS≡△CRQ$,

$$AP=CR \qquad and \qquad AP∥CR.$$

In other words, the quadrilateral $APCR$ is a parallelogram.

Therefore, we can see that $PR$ also passes through the midpoint $M$ of $AC$.

However, $BD$ and $AC$ intersect at $M$.

Therefore, $AC, \ BD, \ PR$ and $SQ$ pass through the same point.