If the midpoints of opposite sides $AB$ and $CD$ of a parallelogram $ABCD$ are $E$ and $F$ respectively, then the quadrilateral formed by the four straight lines connecting these two points and both ends of the opposite sides is also a parallelogram.

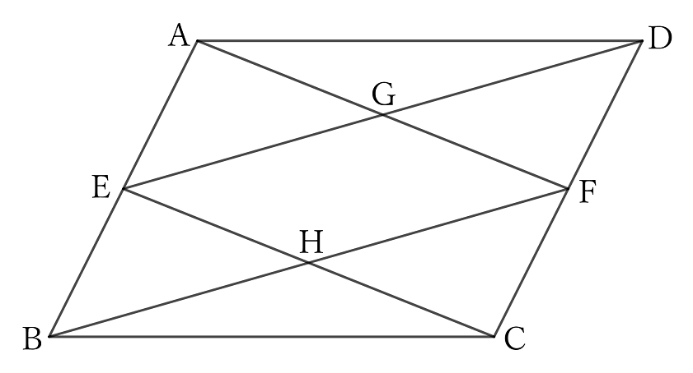
For $△ADF$ and $△CBE$,
$$AD=CB, \qquad DF=BE \qquad and \qquad ∠ADF=∠CBE,$$
$$∴ \quad △ADF≡△CBE,$$
$$∴ \quad ∠FAD=∠ECB,$$
$$∴ \quad AF∥CE,$$
$$∴ \quad FG∥EH. \qquad [1]$$
Similarly, for $△ADE$ and $△CBF$,
$$AD=CB, \qquad AE=CF \qquad and \qquad ∠DAE=∠BCF,$$
$$∴ \quad △ADE≡△CBF,$$
$$∴ \quad ∠ADE=∠CBF,$$
$$∴ \quad DE∥BF,$$
$$∴ \quad GE∥HF. \qquad [2]$$
From $[1]$ and $[2]$, the quadrilateral $GEHF$ is a parallelogram.