Problem
There is one and only one straight line that passes through a point $O$ on a straight line $AB$ and is perpendicular to $AB$.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
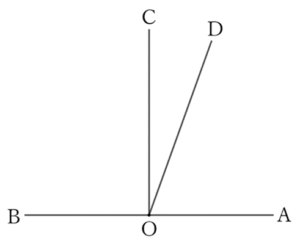
When we draw a straight line $OC$ that bisects the flat angle $∠AOB$, both tangent angles $∠COA$ and $∠COB$ become $∠R$.
Therefore, $CO$ is perpendicular to $AB$.
Next, if in addition to $CO$ there is a straight line $DO$ that passes through $O$ and is perpendicular to $AB$, then
$$∠DOA=∠R.$$
However,
$$∠COA=∠R,$$
$$∴ \ ∠DOA=∠COA.$$
Therefore, since $DO$ overlaps $CO$, there is only one straight line that passes through $O$ and is perpendicular to $AB$.
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.5