Problem
If there are two angles $∠AOB$ and $∠COD$ with the same vertex, and $AO⊥CO$ and $BO⊥DO$, then
$∠AOB=∠COD \quad$ or $\quad ∠AOB+∠COD=2∠R$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
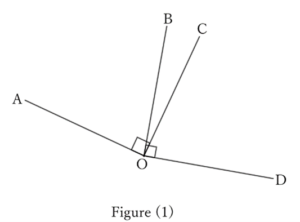
In figure (1),
$$∠AOC=∠BOD (=∠R).$$
Therefore, if we subtract $∠BOC$ from both sides, we get
$$∠AOB=∠COD.$$
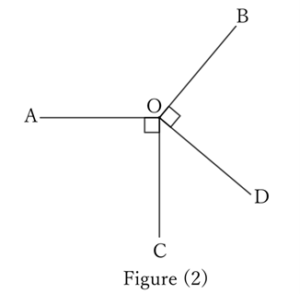
In figure (2),
$$∠AOB+∠BOD+∠COD+∠AOC=4∠R.$$
Since $∠AOC$ and $∠BOD$ are right angles respectively,
$$∠AOB+∠COD=2∠R.$$
$ $
$ $
$ $
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.5