Problem
When the tangent angles $∠AOC$ and $∠BOC$ are complementary angles to each other, let the bisectors of $∠AOC$ and $∠BOC$ be $OD$ and $OE$ respectively. Then,
$$OD⊥OE.$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
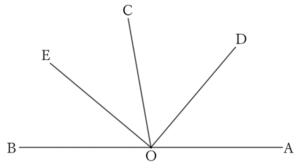
The sum of the tangent angles $∠AOC$ and $∠BOC$ is two right angles, so the sum of the angles that bisect each of these is a right angle. That is,
$$∠DOC+∠COE=∠R.$$
$$∴ \ OD⊥OE.$$
$ $
$ $
$ $
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.6