Problem
If the bisectors $OM$ and $ON$ of the tangent angles $∠AOB$ and $∠BOC$ are perpendicular to each other, $OA$ and $OC$ form a straight line.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
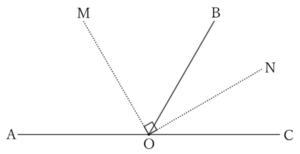
First, from the problem statement,
$$∠AOM=∠MOB.$$
$$∠NOB=∠NOC.$$
By assumption,
$$∠MON=∠R,$$
$$∴ \ ∠MOB+∠NOB=∠R,$$
$$∴ \ (∠AOM+∠MOB)+(∠NOB+∠NOC)=2∠R,$$
$$∴ \ ∠AOB+∠BOC=2∠R,$$
$$∴ \ ∠AOC=2∠R.$$
Therefore, $OA$ and $OC$ form a straight line.
$ $
$ $
$ $
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.6