Problem

---

$$ $$

$$ $$

$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$

$$ $$

$$ $$

$$ $$

$$ $$

$$ $$

$$ $$

$$ $$

$$ $$

$$ $$

$$ $$

---

Solution

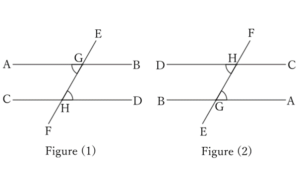
Let the two straight lines be $AB$ and $CD$, and the single straight line that intersects them at $G$ and $H$, respectively, be $EF$.

When $∠AGH=∠GHD$,

$$∠GHC=∠BGH.$$

Therefore, we can rotate the figure (1) to form the figure (2) and overlay it on top of the figure (1) to completely overlap $HD$ on $GA$ and $GB$ on $HC$.

Therefore, if $AB$ and $CD$ intersect on the same side of $EF$, for example, on the side of $B$ and $D$, then the parts of $GA$ and $HC$ in figure (2) that overlap with figure (1) will also intersect.

Therefore, $GA$ and $HC$ in figure (1) also intersect.

In the end, $AB$ and $CD$ intersect on both sides of $EF$.

Then, the two straight lines will intersect at two points, which is irrational.

Therefore, $AB$ and $CD$ never intersect,

$$AB∥CD.$$ 

---

Reference

Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2^nd edition), Seikyo-Shinsha, pp.6-7