Problem
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
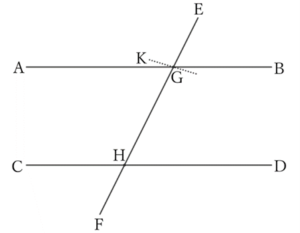
Let $AB∥CD$, and suppose that there is a straight line $EF$ that intersects $AB$ and $CD$ at $G$ and $H,$ respectively, and that $A$ and $C$ are on the same side of $EF$.
(1) If the alternate angles $∠AGH$ and $∠GHD$ are not equal, then we can create $∠HGK$, which is equal to $∠GHD$ and is an alternate angle on it.
Then, $KG$ and $CD$ have the alternate angles which are equal, so they become parallel to each other.
However, there are two straight lines $AB$ and $KG$ that pass through the point $G$ on $AB$ and are parallel to $CD$, which is unreasonable because it violates the axiom.
Therefore,
$$∠AGH=∠GHD.$$
(2) Also, if the corresponding angles $∠AGH$ and $∠CHF$ are not equal, we can create $∠KGH$ that is equal to $∠CHF$ and is a corresponding angle on it.
Then, there are two straight lines $AB$ and $KG$ that pass through the point $G$ on $AB$ and are parallel to $CD$, which is unreasonable because it violates the axiom.
Therefore,
$$∠AGH=∠CHF.$$
(3) If the interior angles on the same side $∠AGH$ and $∠CHG$ do not form complementary angles to each other, we can create $∠KGH$ that passes through the point $G$ on $AB$ and forms a complementary angle to $∠CHG$.
Then, there are two straight lines $AB$ and $KG$ that pass through the point $G$ on $AB$ and are parallel to $CD$, which is unreasonable because it violates the axiom.
Therefore, the interior angles on the same side $∠AGH$ and $∠CHG$ are complementary angles to each other:
$$∠AGH+∠CHG=2∠R.$$
(4) Similarly, the exterior angles on the same side $∠AGE$ and $∠CHF$ can also be said to form complementary angles as shown below:
$$∠AGE=2∠R-∠AGH,$$
$$∠CHF=2∠R-∠CHG,$$
$$\begin {eqnarray} & & ∴ \ ∠AGE+∠CHF\\ &=& 2∠R-∠AGH+2∠R-∠CHG\\ &=& 4∠R-(∠AGH+∠CHG)\\ &=& 4∠R-2∠R\\ &=& 2∠R.\end {eqnarray}$$
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.7