Problem
When three straight lines $a, b$ and $c$ are on the same plane, and $a∥b$ and $a∥c$, then
$$b∥c.$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
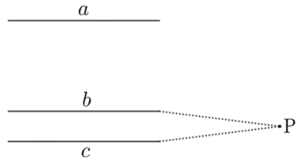
Assuming $b∦c$, two straight lines that are not parallel will always intersect on the same plane.
Now, if the point of intersection is $P$, then $P$ is always outside $a$.
Thus, there are two straight lines $b$ and $c$ that pass through this point $P$ and are parallel to $a$, but this contradicts the axiom.
Therefore, $b$ and $c$ never intersect,
$$b∥c.$$
$ $
$ $
$ $
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.7