Problem
When a straight line $EF$ cuts across parallel lines $AB$ and $CD$, the bisectors of the alternate angles and the corresponding angles are parallel.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
(1) In the figure below, $AB∥CD$, and $∠AEF$ and $∠EFD$ form the alternate angles.
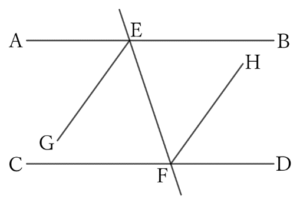
Thus,
$$∠AEF=∠EFD,$$
$$∴ \ \frac{1}{2}∠AEF=\frac{1}{2}∠EFD,$$
$$∴ \ ∠GEF=∠EFH,$$
$$∴ \ EG∥FH.$$
(2) In the figure below, $AB∥CD$, and $∠GEB$ and $∠GFD$ form the corresponding angles.
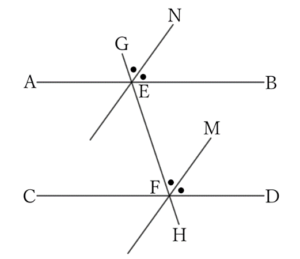
Therefore,
$$∠GEB=∠GFD,$$
$$∴ \ \frac{1}{2}∠GEB=\frac{1}{2}∠GFD,$$
$$∴ \ ∠GEN=∠GFM,$$
$$∴ \ EN∥FM.$$
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.8