Problem
When two line segments $AB$ and $CD$ are parallel to each other in the same direction, if we take a point $P$ that is not between $AB$ and $CD$, then
$$|∠ABP-∠CDP|=∠BPD.$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
(1) Suppose that $P$ is on the side of $AB$ with respect to $CD$.
If we draw a parallel line $PQ$ from $P$ in the same direction as $AB$, we have
$$∠BPQ=∠ABP, \qquad ∠DPQ=∠CDP.$$
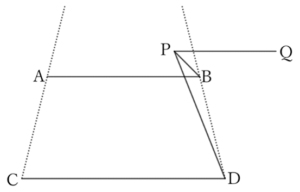
As shown in the above figure, when $∠DPQ>∠BPQ$,
$$∠DPQ-∠BPQ=∠BPD,$$
$$∴ \ ∠CDP-∠ABP=∠BPD. \qquad [1]$$
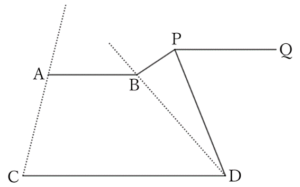
As shown in the above figure, when $∠DPQ<∠BPQ$,
$$∠BPQ-∠DPQ=∠BPD,$$
$$∴ \ ∠ABP-∠CDP=∠BPD. \qquad [2]$$
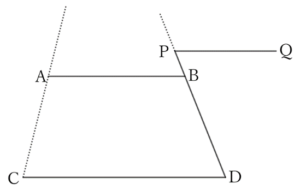
As shown in the figure above, when $∠DPQ=∠BPQ$,
$$∠BPQ-∠DPQ=0=∠BPD,$$
$$∴ \ ∠ABP-∠CDP=∠BPD. \qquad [3]$$
From $[1], [2]$ and $[3]$,
$$|∠ABP-∠CDP|=∠BPD.$$
(2) The same proof can be given when $P$ is on the side of $CD$ with respect to $AB$.
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.9