Problem
When two sides of a triangle are unequal, the angle opposite the longer side is greater than the angle opposite the shorter side.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
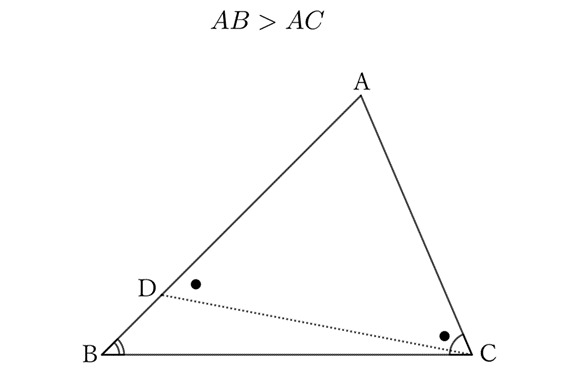
Suppose $AB>AC$ in $△ABC$.
If we take $AD$ equal to $AC$ on $AB$, then since $AB>AC$, $D$ is on the side $AB$.
Connecting $C$ and $D$, we get
$$∠ADC=∠ACD.$$
However, because $∠ADC$ is one exterior angle of $△DBC$, it is larger than $∠B$.
$$∴ \ ∠ACD>∠B.$$
On the other hand,
$$∠ACB \ (=∠C)>∠ACD,$$
$$∴ \ ∠C>∠B.$$
$ $
$ $
$ $
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, pp.11-12