Problem
If two sides of one triangle are equal to two sides of another triangle, but the third sides are unequal, the angle opposite the larger side is greater than the angle opposite the smaller side.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
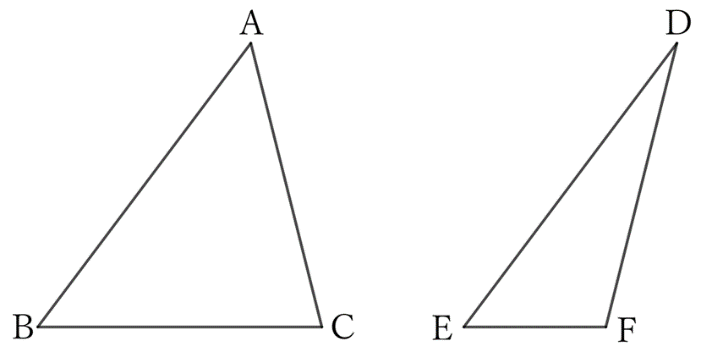
Let $AB=DE, \ AC=DF$, and $BC>EF$.
If $∠A=∠D$, the pairs of sides and their included angles are equal.
Thus, since $△ABC≡△DEF$,
$$BC=EF,$$
which violates the assumption.
$$∴ \ ∠A≠∠D.$$
If $∠A<∠D$, from the previous problem $0040$,
$$BC<EF,$$
which is also against the assumption.
$$∴ \ ∠A≮∠D.$$
Since $∠A≠∠D$ and $∠A≮∠D$,
$$∠A>∠D.$$
$ $
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.12