Problem
When we take any two points $P$ and $Q$ inside or on the circumference of $△ABC$, the length of line segment $PQ$ does not exceed the length of the maximum side of this triangle.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
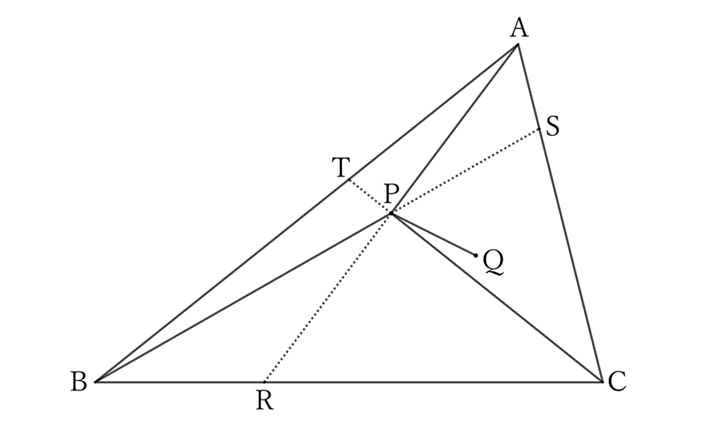
If $AB≥BC≥CA$, and the point where the extension of $AP$ intersects with $BC$ is $R$, then from the previous question $0043$,
$$AB≥AR≥AP.$$
Similarly,
$$AB≥BS≥BP.$$
$$AB≥BC≥CT≥CP.$$
Therefore, $AP, \ BP$, and $CP$ do not exceed $AB$.
Now, if $Q$ is within $△APC$, similarly, $PQ$ does not exceed the maximum side of $△APC$.
By the way, the maximum side of $△APC$ does not exceed $AB$. Thus,
$$PQ≤AB.$$
$ $
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.13