Problem
In $△ABC$, if the bisector of $∠A$ is $AN$ and the perpendicular line from $A$ to $BC$ is $AH$, then
$$∠HAN=\frac{1}{2} |∠B-∠C|$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
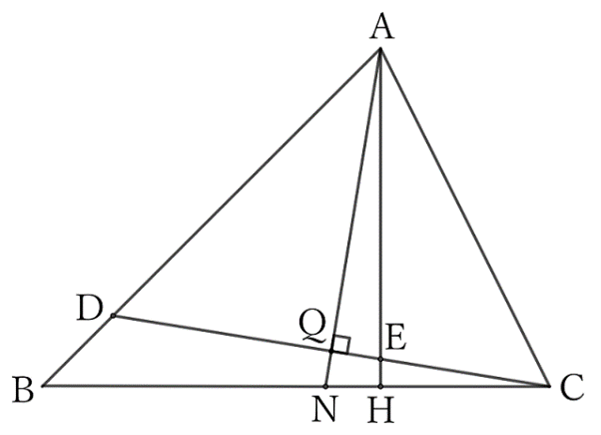
When $AB>AC$, take the point $D$ on $AB$ such that $AD=AC$, and let the intersection of $CD$ and $AH$ and that of $CD$ and $AN$ be $E$ and $Q$, respectively.
Since $△ACD$ is an isosceles triangle, the bisector $AQ$ of $∠A$ is perpendicular to $CD$.
Now, regarding $△AEQ$ and $△CEH$,
$$∠AEQ=∠CEH \qquad and \qquad ∠AQE=∠CHE \ (=∠R).$$
$$∴ \ △AEQ \sim △CEH,$$
$$∴ \ ∠EAQ=∠ECH,$$
$$∴ \ ∠HAN=∠BCD.$$
However, from the previous question 0055, when $AB>AC$,
$$∠BCD=\frac{1}{2} (∠C-∠B),$$
$$∴ \ ∠HAN=\frac{1}{2} (∠C-∠B).$$
Similarly, when $AB<AC$,
$$∠HAN=\frac{1}{2} (∠B-∠C).$$
Also, if $AB=AC$,
$∠B=∠C$ and $AH$ and $AN$ overlap.
Thus,
$$∠HAN=\frac{1}{2} (∠B-∠C)=0.$$
Therefore, in any case,
$$∠HAN=\frac{1}{2} |∠B-∠C|.$$
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.15