Problem
Create an isosceles triangle $ALM$ that overlaps two sides $AB$ and $AC$ of a triangle $ABC$, extend $LM$ and $BC$, and let $N$ be their intersection. Then the straight line $LN$ intersects $AB$ at an angle equal to half the sum of its lower angles, and intersects the extension of the base of the triangle $ABC$ at an angle equal to half the difference of its lower angles.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
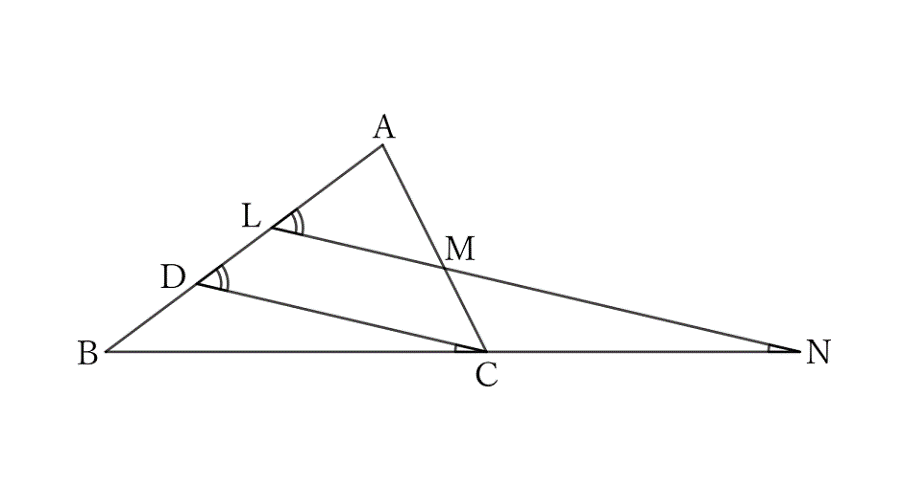
Let $AB>AC$, and if we draw $CD$ parallel to $LM$ through $C$, we have
$$AM=AL,$$
$$∴ \ AC=AD.$$
Then, from the problem $0055$,
$$∠ADC=\frac{1}{2} (∠B+∠C) \qquad and \qquad ∠DCB=\frac{1}{2} (∠C-∠B).$$
And since $LN∥DC$,
$$∠ALM=∠ADC=\frac{1}{2} (∠B+∠C) \qquad and \qquad ∠N=∠DCB=\frac{1}{2} (∠C-∠B).$$
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.15