Problem
If we drop a perpendicular line $AB$ to the straight line $XY$ from a point $A$ that is not on $XY$, and draw hypotenuses $AC$, $AD$ and $AE$ on the same side as $AB$ so that $∠BAC$, $∠CAD$ and $∠DAE$ are equal, we have
$$CB<DC<ED.$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
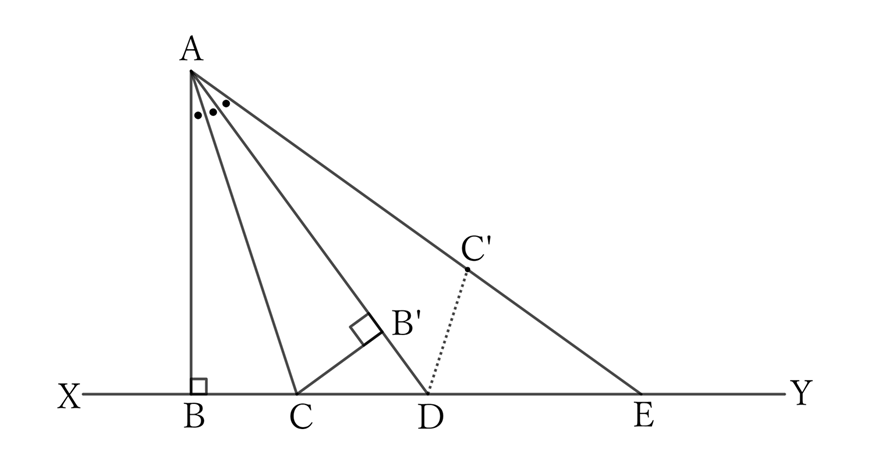
Since $AB$ is a perpendicular line, and $AC$, $AD$ and $AE$ are hypotenuses,
$$∠R>∠ACB>∠ADC,$$
$$∴ \ ∠R<∠ACD<∠ADE.$$
Therefore, if we draw $CB’$ and $DC’$ so that $CB=CB’$ and $DC=DC’$, $CB’$ and $DC’$ fall within $∠ACD$ and $∠ADE$, and
$$△ACB≡△ACB’ \qquad and \qquad △ACD≡△AC’ D.$$
$$∠CB’ D \ (=∠R)>∠ADC,$$
$$∴ \ CB'<DC,$$
$$∴ \ CB<DC. \qquad [1]$$
$$∠DC’ E=∠ACB,$$
$$∠ACB>∠DEC’,$$
$$∴ \ ∠DC’ E>∠DEC’,$$
$$∴ \ DC'<ED,$$
$$∴ \ DC<ED. \qquad [2]$$
From $[1]$ and $[2]$,
$$CB<DC<ED.$$
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.17