Problem
In an acute triangle $ABC$, let $∠B=2∠C$ and $AH⊥BC$. When $AB$ is extended to $D$ so that $BD=BH$, the extension of $DH$ passes through the midpoint $M$ of $AC$.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
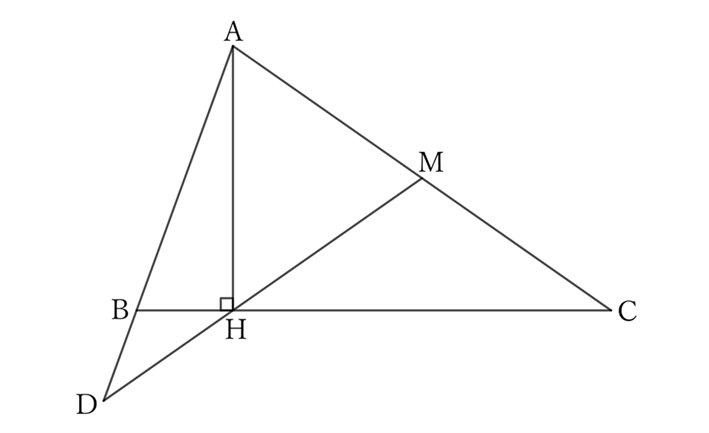
If $∠C=θ$, then
$$∠B=2θ.$$
Since $BD=BH$, the triangle $BDH$ is an isosceles triangle with $B$ as the vertex, and since the exterior angle of $∠HBD$ is $2θ$,
$$∠BDH=∠BHD=θ,$$
$$∴ \ ∠MHC=θ.$$
Therefore, since the triangle $MCH$ is an isosceles triangle with $M$ as the vertex,
$$MC=MH. \qquad [1]$$
Regarding the triangle $MAH$,
$$∠HMA=2θ \qquad and \qquad ∠MHA=∠R-θ,$$
$$∴ \ ∠MAH=2∠R-2θ-(∠R-θ)=∠R-θ.$$
Therefore, since the triangle $MAH$ is an isosceles triangle with $M$ as the vertex,
$$MA=MH. \qquad [2]$$
From $[1]$ and $[2]$,
$$MA=MC.$$
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.17