Problem
In an acute triangle $ABC$, take points $P$ and $Q$ on the perpendicular lines drawn from the vertices $B$ and $C$ to the opposite sides, or on their extensions, so that $BP=CA$ and $CQ=BA$, respectively. Also, if we take points $P’$ and $Q’$ on $BC$ so that $PP’⊥BC$ and $QQ’⊥BC$, then
$$PP’+QQ’=BC$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
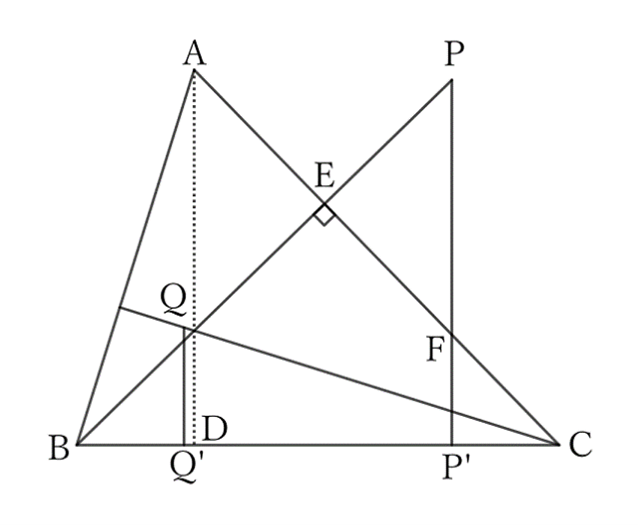
Regarding $⊿ABD$ and $⊿CQQ’$,
$$AB=CQ \qquad and \qquad ∠ADB=∠CQ’ Q \ (=∠R).$$
Furthermore, since $∠BAD$ and $∠QCQ’$ are both complementary angles of $∠B$,
$$∠BAD=∠QCQ’,$$
$$∴ \ ⊿ABD≡⊿CQQ’,$$
$$∴ \ QQ’=BD.$$
Regarding $⊿PFE$ and $⊿CFP’$,
$$∠PFE=∠CFP’ \qquad and \qquad ∠PEF=∠CP’ F \ (=∠R).$$
$$∴ \ ⊿PFE〜⊿CFP’,$$
$$∴ \ ∠EPF=∠P’ CF.$$
Regarding $⊿CAD$ and $⊿PBP’$,
$$BP=CA, \quad ∠CDA=∠PBP’ \quad and \quad ∠DCA=∠P’ PB,$$
$$∴ \ PP’=CD,$$
$$∴ \ CD+BD=BC,$$
$$∴ \ PP’+QQ’=BC.$$
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, pp.17-18