Problem
In a triangle $ABC$, let $∠B<∠C$ and draw the perpendiculars $BD$ and $CE$ from $B$ and $C$ to their opposite sides, respectively. Then, we have
$$CE>BD.$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
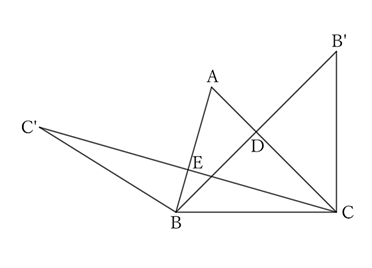
If we extend $BD$ and take a point $B’$ such that $BD=DB’$, and extend $CE$ and take a point $C’$ such that $CE=EC’$, then $△BCB’$ is an isosceles triangle with $C$ as the vertex, and $△CBC’$ is an isosceles triangle with $B$ as the vertex, and
$$BC’=BC=CB’.$$
Moreover,
$$∠CBC’=2∠B \qquad and \qquad ∠BCB’=2∠C.$$
Since we assume $∠B<∠C$,
$$∠CBC’>∠BCB’.$$
Since $△BCB’$ and $△CBC’$ share the side $BC$, and $CB’=BC’$ and $∠CBC’>∠BCB’$,
$$CC’>BB’.$$
However,
$$CE=\frac{1}{2} CC’ \qquad and \qquad BD=\frac{1}{2} BB’,$$
$$∴ \ CE>BD.$$
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.18