Problem
Let $O$ be the intersection of the bisectors of $∠B$ and $∠C$ of a triangle $ABC$, and let $M$ and $N$ be the intersections of $AB$ and $AC$ with a straight line drawn through $O$ parallel to $BC$, respectively. Then,
$$MN=MB+NC.$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
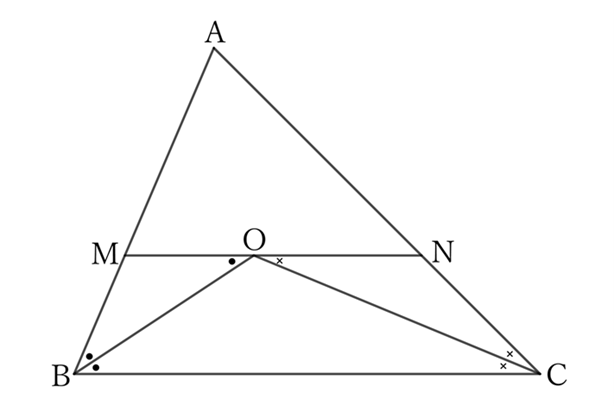
Since $MN∥BC$,
$$∠MON=∠OBC.$$
By definition,
$$∠MBO=∠OBC,$$
$$∴ \ ∠MBO=∠MOB.$$
Therefore, since $△MBO$ is an isosceles triangle with $M$ as the vertex,
$$MO=MB.$$
Similarly,
$$∠NOC=∠OCB.$$
By definition,
$$∠NCO=∠OCB,$$
$$∴ \ ∠NCO=∠NOC.$$
Therefore, since $△NCO$ is an isosceles triangle with $N$ as the vertex,
$$NO=NC.$$
However,
$$MN=MO+NO,$$
$$∴ \ MN=MB+NC.$$
$ $
$ $
$ $
Reference
Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, pp.18-19